Sortbot demonstrates sorting
The little sortbot demonstrates quicksort and insertion sort, which are two of the most common ways computers use to sort a list. How do the two methods differ? Which one is best?
About sorting

Sorting means putting a list into order
Sorting is something computers need to do a lot. Why? Because one of the tricks for finding things efficiently is to sort them first, and humans often want computers to find things quickly.
Programmers (and computer scientists) like to think about how sorting works because it’s an important yet straightforward problem that — on the face of it — is easy to understand. The underlying question they are usually asking is “what’s the best way to perform a sort?”

It depends on a number of factors, including what you mean by “best”, and, perhaps more subtly, what you know about the list before you start.
Most people don’t think about this. But if you do, and you’re interested in how something as straightforward as sorting a pack of playing cards might be automated... well, you should be a programmer.
What you need to do a sort:
- a list of things
- the order those things should be in
Often, both these are easy. For example, to sort a pack of cards:
things
(also called data, or inputs)

What cards are in the pack?
For example:
French playing cards
(pips and Jack/Queen/King picture cards) without jokers
order
(what goes before what?)

What rules define the right order?
For example:
suit order
♣ → ♦
→ ♥ → ♠,
within suit, by value with
aces low
Comparing things
The principle behind this kind of sorting is that the order emerges from making comparisons between any two items on the list. “Should this thing come before or after that thing?”
This might not be obvious unless you’ve thought about computation before. You can’t simply compare two lists: the method for doing that has to be built up from the computer’s (current) limitation of only being able to look at one thing at a time (although... well, read through to the end).
Often, the comparison is straightforward: for example, if the inputs are numbers, then negative numbers come before positive numbers, and small numbers before big ones (but what about complex numbers, or coordinate points?). For words or names, alphabetic order seems obvious (but what about 官话? Or the letters that come after Z?).
Sometimes explicit rules are needed. If the inputs are playing cards then there are two common conventions on how to order suits. But that’s OK, provided you agree which one you want before you start. The sortbot uses the ♣♦♥♠ order, which (in English) happens to be alphabetical too. (But if there were jokers in the pack, where should they go?)
But what if you’re sorting colours? Or genomes? Or sounds? All these things might need to be sorted. In each case the comparison operation is something you need to be clear about before you can sort your things.
In fact, there are other ways of thinking about sorting. But comparison sorting is the most common and practical approach.
The comparison function
The result of comparing two things on the list is the answer “before” or “after”, because it’s really asking “should this thing go before or after that thing in the list?”

Three of clubs goes before six of clubs

Queen of clubs goes after six of clubs
In computing terms there are really three answers, because a third possibility is that both this thing and that thing belong in the same place: that can happen if the two things are equal.
So a comparison can provide one of three results:

This kind of comparison function effectively takes any two things and
returns one of those three possible results, indicating the first
thing’s position relative to the second. For convenience, the results
are often mapped to −1, 0 or
+1. It’s sometimes represented in programming
languages as an operator that sits between the two items (the
operands) with the “spaceship” symbol <=>.
Counting comparisons
So, in order to sort a list, you must be able to define a function that can make that comparison. The act of making each comparison between two things is the basic unit of measurement for sorting methods, because usually it’s true to say everything else (how you move through the list and what you do once you’ve made a comparison) more or less evens out between different methods.
The goal is to find a way to sort your things by minimising the number of comparisons you have to make. In effect, the cost of a sorting algorithm is measured by how many comparisons it makes.
Very broadly speaking, the best sorting method makes the fewest comparisons. The catch is, as the demonstrations show, that the number of comparisons often depends on the initial order of the (potentially shuffled) inputs.
Sort the things, sort the list
Trying to minimise the number of comparisons only makes sense if it’s possible to sort a list without needing to compare every thing with every other thing. If that wasn’t true, then you’d always need to compare all the things, and there wouldn’t be any scope to do fewer comparisons.
The magic here is knowing that if this is less than that, and that is less than all those, then you can infer that this is less than those too. If a property has this quality, then it is called transitive.
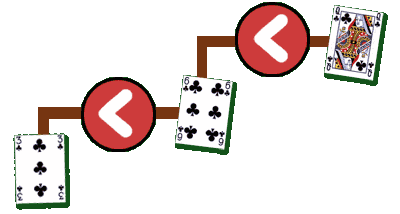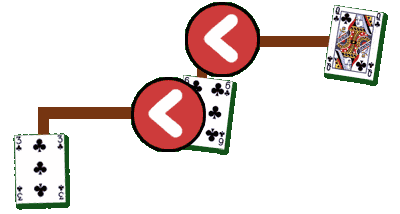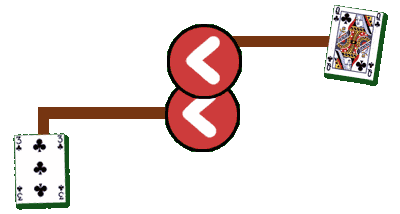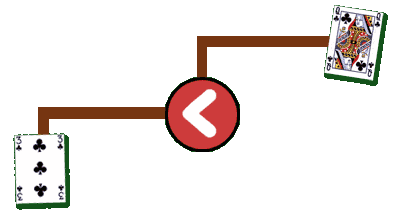
three of clubs < six of clubs
six of clubs < queen of clubs
therefore
three of clubs < queen of clubs
Comparisons that are not transitive do exist, but are unusual. The game rock, paper, scissors is an example: every item is less than and greater than the others, which means you can’t truthfully sort them into a list using the game’s rules for comparing things (instead, you end up with a list that loops back around on itself... forever). Of course, you can sort “paper, rock, scissors” into a well-ordered list, but you have to change the comparison to one that is transitive in order to do it (in that case, just then, it was alphabetic).
Size of input
The number of comparisons you make when you’re sorting a list will depend on how many things there are in the list. The longer the list, the more comparisons. That probably seems obvious.
The number of inputs (which traditionally is written as n) is the technical way of saying how long the list of things to be sorted is.
So what people are really looking for when they wonder if their method of sorting is good is how does the number of comparisons change as the number of inputs gets bigger?
This is a sneakily complex question, because the answer may depend on what kind of circumstances you’re interested in. The best-case and worst-case performances of a given sort algorithm may be significantly different from its general case. And what might trigger best- and worst-case might be related to things you know in advance about the data that is to be sorted.
But, very roughly, the sort of answer you can expect describes the curve of the graph of number-of-inputs (n) plotted against the number of comparisons that will/might/must be needed to complete the sort (those details are the sneaky part). Generally, the more steeply the curve climbs as the inputs increase, the more complex the algorithm is.
Why does complexity matter?
Sometimes it doesn’t.
But often it does, and sometimes it can be critically important. Usually (although not always) this is about time.
Computers run at finite speeds, so a complex method requiring many comparisons will need more time to run to completion than a simpler one needing fewer.
There are two common ways in which this can matter: either the time or resources you have available are tightly constrained (such as in real-time applications like games where you might need to perform entire sorts in the few milliseconds between video frames), or else the number of inputs is huge (such as astronomical data sets that might require days or weeks of processing).
Of course, this applies to a wide range of applications, not just sorting.
Two example algorithms
An algorithm is really just a clearly-specified method that, if followed step-by-step, will result in a solution. So a sorting algorithm starts with inputs (a shuffled pack of cards) and ends up with them sorted.
A program implements the algorithm. So the distinction between the algorithm and the program is a useful one: the algorithm describes, step-by-step, how the problem is to be solved. The program is a set of instructions that the computer must follow in order to execute that algorithm. Two programmers can write two quite different programs than implement the same algorithm.
So here is the sortbot following instructions that implement two of the most common sorting algorithms. As well as seeing how they work, you can investigate the average number of comparisons per card that the bot makes. How does it change as you vary the number of cards or their initial order?
Example 1: Insertion Sort

The insertion sort is a simple way of sorting. It’s probably the closest way to how you’d do it if you had the cards in your hand right now. (The reason you wouldn’t do it quite this way is because your brain doesn’t need to follow a rigid formal method, and is especially good at noticing patterns and shortcuts of more than one card at the same time).
Insertion sort more or less works by taking each card (input) and comparing it with each of the cards in the list of cards you’ve already sorted, and stopping as soon as you get to either a card which goes after this one, or the end of the stack. Insert the card into the stack at this position. Repeat until you’ve got no cards left to sort.
The sortbot’s insertion sort
The sortbot is demonstrating the simplest form of insertion sort, by starting at the top of the ever-growing list of sorted cards, and working along it comparing as it goes. If you watch you should notice there’s something inefficient about this, because as the chain gets longer, when the bot has a high-value card, it spends a lot of time making comparisons with cards that are at the low-value end.
However, in one particular circumstance this is the most efficient sort: if the inputs are already in reverse order, each card is put into position with a single comparison.
run insertion sort on reverse-order cards
Binary chop
One well-known way of making the sort more efficient is for the bot to start by going to the middle of the (ever-growing) list of sorted cards, instead of always from one end (which, perhaps half the time, will be a bad decision). After each comparison, it goes to the middle of the remaining portion of the list, left or right. This is called a binary chop (because it’s chopping the available options into two, and thereby dismissing half of the remaining cards with each chop).
run insertion sort with binary chop
Once there are over a handful of cards in the sorted list that emerges, you can see the sortbot seeking the insertion point by jumping into the middle of the list instead of stepping along, one card at a time, from the top.
The binary chop is also known as a binary search: it’s the most generally efficient way of finding something in a set, but it depends on that set being well-ordered. That makes sense here because, after all, the sortbot is really searching for the insertion point in a list which it knows to be well-ordered... because it is the sorted list that it is producing.
You’d expect the binary chop to be more efficient (that is, require fewer comparisons per input) than the basic method of stepping along every card in the list looking for the insertion point. But actually (especially if you use the default shuffle the sortbot provides) you might discover it’s not quite that simple: sometimes you get a better result without the binary chop.
The problem is that the number of comparisons is directly affected not only by the number of inputs but also the order they start in. This is why the analysis of computational complexity is not straightforward.
As you increase the number of cards (right up to the full 52-card pack) you can start to see a clearer pattern emerge. You might be able to see up to ten times as many comparisons per card when not using the binary chop.
Example 2: Quicksort

The quicksort method works like this:
You take the first card off the inputs and declare it “the pivot”. Then you compare each card with that pivot and put it in a pile to the left or the right of that pivot card, depending on whether it goes before or after.
When you’ve done that, you’ve now got two piles (one on the left, one on the right) and the pivot card. So you simply repeat the same process with each of those piles.
Inevitably, as you go through this process, effectively removing one pivot from each pile as you go split them apart, the piles get smaller and smaller... until they contain only one card (or perhaps none at all, which isn’t really a pile at all).
When all your piles only have one card, well, you’ve finished. Your piles are in order.
You can see this when the bot performs the sort. When it’s finished, it collects the cards. In practice this stage isn’t needed, because efficient sorts put the cards in the right place as they go. The demonstration doesn’t do that until the end, so you can see how the method is breaking the inputs down into those piles.
Some details and complexities
If you watch how the number of comparisons builds up — especially the number of comparisons per input (that is, per card) — you might spot a pattern. Try sorting cards that are already in sorted order (or in reverse sorted order). You’ll see the shape of the graph that the bot makes is quite distinct, and the number of comparisons per input gets high.
run quicksort on a reversed list
Choosing the pivot
It turns out that quicksort is at its most efficient when the tree-like graph of those piles is well-balanced. Strictly speaking, the sort works best if the pivot always has the middle-value of the cards in the pile. (You can see when this happens, because the bot will end up with two piles either side of that pivot with roughly the same number of cards in each — this is why it’s called “well-balanced”.) The paradox is that the bot can’t pick that card without doing comparisons, which is exactly the operation you’re trying not to do unnecessarily.
So in effect, by using this method the bot is gambling on picking a good pivot more often than not. That’s not a bad strategy, provided the input is truly unpredictable (that is, the cards really have been shuffled).
Unless you tell it otherwise, the sortbot in the demo is simply taking the first card off the pile and using that as the pivot. That makes sense if those inputs really are in random order, because in a shuffled pack picking any one card is as blind as picking any other.
But here’s the odd thing. If the bot were to pick the middle card, or a random card, as its pivot, that would lessen the inefficiency of sorting a list that is already sorted (or reversed). Whether that behaviour is needed really depends on how likely it is that such an input is expected.
For a sorted list, changing the way the pivot is chosen makes a difference even with just a few cards, as these examples show:
So when deciding which sort is best, you need to know how badly ordered the inputs are likely to be. If you know that sections of the input will be well-ordered then you may be better off using another method entirely which, unlike quicksort, can exploit that to minimise comparisons. In a casino, you can expect cards being dealt from a shuffled deck to be poorly ordered. But in real world cases — maybe where the sort happens when one or two new inputs have been added to the end of existing data — you can sometimes confidently predict that large parts of the input will be coming at you in good order.
Adding inputs after the sort has started
What would happen if you dropped more cards into the input pile once the bot has started sorting?
For the demo this is not a problem because once you press GO you simply cannot add more cards. But in some applications, it may be important that you can introduce more inputs to a sort that has already commenced.
Once the bot has started quicksort, you can’t easily add any new cards as input, because they have missed being put into the right piles either side of the pivots that the sortbot has already chosen, and the sortbot only works with cards in piles below the pivots.
But if you’re using insertion sort, it wouldn’t be a problem. If you add an extra input once the sort has started, the sortbot wouldn’t notice, because it returns to the input pile again and again.
Hybrid sorts
For a small number of inputs, insertion sort is generally more efficient than quicksort. So some implementations of quicksort switch to using an insertion sort on any pile with less than ten cards in it.
Parallelism
Could you make the sort more efficient if you had more bots?
Because quicksort is really just about sorting piles, it’s a good candidate for parallelism. As soon as the bot has finished splitting a pile into two around its pivot, each of those new piles can be sorted wholly independently of the other. That is, after each pivot, you could add an extra bot. The bots can set about sorting their own piles at the same time: in parallel.
So in an environment where there are multiple processors available, the restriction on making comparisons between any two inputs at a time does not prevent the work of sorting the whole list being shared out as the sort progresses.
Stable sorts
What happens when two inputs have the same value? In a standard pack of cards this can’t happen, because every card is unique and there are no duplicates.
But in other data it may be normal for two inputs to be the same
(that is, the comparison function returns =).
When this happens, a sort is said to be stable if it doesn’t change the order of inputs that are equal.
Playing cards are an example of when a sort does not need to be stable. For example, if all the aces in the pack were aces of spades, you probably don’t care (and, unless they’re marked cards, you can’t even tell) which one of them comes first... provided of course they all end up next to each other in the right place relative to the other cards.
But sometimes it can be important that the order of identical records isn’t changed, so the sort method and the way it’s been implemented may need to guarantee this behaviour.
(The sortbot demo currently doesn’t have any duplicate cards.)
Isn’t sorting a solved problem?
Quicksort was developed by British computer scientist Tony Hoare around 1960.
Lots of programmers today will never need to write a sort algorithm,
because the language or framework they’re using already has one... so
just by calling the sort() method the problem is solved
(and, incidentally, it’s most likely that it will be implementing a
quicksort).
So knowing about sorting isn’t so you can write your own sort routines (although you can). It’s really about understanding the nature of this kind of problem. If you understand how such a straightforward problem can have such a variety of solutions, and how their efficiency differs and how you might find that out, and how computer science begins to analyse complexity... well, then you are probably a good programmer. Perhaps more to the point, if you can’t, then you probably are not.
More information
There’s lots of information about the different sorting algorithms and analysis of their relative merits out there on the web. This demonstration only shows quicksort and insertion sort, but there are many other algorithms, each with its own advantages and disadvantages.
- elegant visual comparisons from sorting.at
- lovely visual comparison of the main algorithms on toptal.com
- Wikipedia page on sorting algorithms is a good jumping-off point
- the big-O cheatsheet is a summary of complexity analysis, which makes it clear how insertion sort can outperform quicksort (...but, of course, it depends)
- see also this explanation of big-O by user cletus on StackOverflow which uses the telephone book (if you remember those) and the Travelling Salesman to help explain things
- Khan Academy on sorting encourages you to implement and think about sorting in Javascript
52-card results
The sortbot’s demo lets you start with a random but fixed pack — that is, the cards are shuffled but are identically shuffled each time you run it (of course, you can also opt to shuffle the cards properly every time if you prefer). These are the sortbot’s results after sorting the full random (but fixed) pack:
Sorted by insertion sort (step along list)
Cards: 52, comparisons: 888 (per card: 17.08)
Sorted by quicksort (first-card pivot)
Cards: 52, comparisons: 464 (per card: 8.92)
Sorted by quicksort (middle-card pivot)
Cards: 52, comparisons: 268 (per card: 5.15)
Sorted by insertion sort (use binary chop)
Cards: 52, comparisons: 254 (per card: 4.88)

About the demo
Quicksort is usually shown operating on an array or flat list (because more often than not that is how it’s implemented). But the underlying method of quicksort — repeatedly splitting the input into two piles either side of a pivot, until the piles are too small to sort any more — is much clearer when presented as a process with a tree-like graph like this. Adrian Johnstone of Royal Holloway CompSci department suggested this in 2012. It took me a while (about 5 years) to getting round to implementing it in the form you see it now. Hopefully when the bot starts flying around the screen, you can see order emerging from chaos (especially because playing cards are so visual), and the simple repetitive method of the sort becomes clear.
- Tech: HTML (especially canvas) and JavaScript using PIXIjs v4
- Playing cards: (via Wikipedia) © Colin M.L.Burnett / Wikimedia Commons / CC-BY-SA-3.0 / GFDL
When the bot does Quicksort, it puts some effort into thinking ahead (in fact, it rehearses the entire sort in its head before it starts), in order to avoid laying the cards out on top of each other. In practical terms, computation doesn’t lay cards out in space like this, so it’s only a problem with the presentation and not the sort. Insertion sort doesn’t present the same layout problem because, as you’ll see if you run it, the tree structure doesn’t emerge in the same way.
Similarly, the sortbot pootles around in the route it does so you can see what’s going on. For this reason, this isn’t a demonstration of relative speed of sorting: it’s showing you how the sort works. Sometimes the sortbot takes the scenic route.